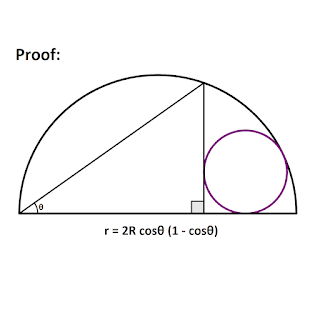
A circle is completely inscribed in a semicircle and separated by a chord that is perpendicular to the diameter of the circle. Radius in terms of radius and angle of inclination of the top of the chord from the end of the diameter.
The radius of the semicircle is 'R' and the radius of the inscribed circle is 'r'.
Also,
Proof:
Let K is the center of the semicircle:
By trigonometry:
\[m = R\cdot \cos(2\theta)\]
\[\Rightarrow m = R(2\cos^2\theta-1)\]
Now consider the triangle KEF,
EF is perpendicular to KE:
\[ KE^2+EF^2=KF^2\]
\[\Rightarrow (m+r)^2+r^2=(R-r)^2\]
\[\Rightarrow (2R\cos^2\theta-R+r)^2+r^2=(R-r)^2\]
\[\Rightarrow r^2+4Rr\cos^2\theta+4R^2\cos^4\theta-4R^2\cos^2\theta=0\]
\[\Rightarrow r^2+r(4R\cos^2\theta)-4R^2\cos^2\theta\sin^2\theta=0\]
It is a quadratic equation on variable r:
\[\Rightarrow r=\frac{-4R\cos^2\theta+\sqrt{16R^2\cos^4\theta+16R^2\cos^2\theta\sin^2\theta}}2\]
\[\Rightarrow r=-2R\cos^2\theta+2R\cos\theta\sqrt{\cos^2\theta+\sin^2\theta}\]
\[\Rightarrow r=2R\cos\theta-2R\cos^2\theta\]
\[\Rightarrow r=2R\cos\theta(1-\cos\theta)\]
In a similar method, the second figure can also be proved in which we will get all terms in sine instead of cosine.